• Accueil
  • Dynamique de transport espace/temps/échelle

Contact:

Fabien THIESSET, chargé de recherches CNRS

Table des matières

Contexte et Motivation
Équations statistiques en deux points
Mesures géométriques intégrales
Écoulements explorés

Contexte

Les écoulements turbulents diphasiques sont multi-échelles et multi-dimensionnels, c’est à dire qui dépendent :

– de la position dans l’écoulement,
– de l’échelle des structures liquides
– des propriétés des fluides

Lorsqu’elles se rompent, ces structures liquides subissent une évolution continue de leur :

– géométrie (surface, courbure),
– morphologie (sphéricité, ligamentarité)
– topologie (connectivité)
– dynamique (singularité aux temps finis)

Motivation

Les facettes multi-échelle et multi-dimensionnelle des écoulements diphasiques requièrent une nouvelle théorie:

– qui tisse un lien avec la géométrie, la morphologie et la topologie de l’interface liquide-gaz,
– qui scrute la dynamique de l’écoulement liquide à la fois dans l’espace des échelles et des positions dans l’écoulement
– qui permet de retrouver un degré de prédictibilité et régularité au sens statistique.

Rendu réaliste du champ liquide dans une couche de cisaillement diphasique simulée par le code ARCHER.

Schematic representation of the phase indicator field \phi. Gray zones represent the liquid phase (\phi=1), white zones the gas phase (\phi=0). The two points \boldsymbol{x^+} and \boldsymbol{x^-} together with the mid-point \boldsymbol{X} and the separation vector \boldsymbol{r} are also sketched.

Équations statistiques en deux points

Dans cette perspective, nous proposons d’utiliser la machinerie des équations statistiques en deux points telle que développée dans le cadre des écoulements turbulents monophasiques et qui est adaptée ici à un scalaire pertinent des écoulements diphasiques : la fonction indicatrice de phase \phi. Cette variable de champ est définie:

(1)   \begin{equation*} \phi(\boldsymbol{x}) = \left\{ \begin{array}{ll} 1 \textrm{~~~dans la phase liquide} \\ 0 \textrm{~~~dans la phase gaz} \end{array} \right. \end{equation*}

L’équation de transport de \phi se lit

(2)   \begin{equation*} \partial_t \phi + \boldsymbol{u} \cdot \boldsymbol{\nabla_x} \phi =0 \end{equation*}

En écrivant l’Eq. (2) en deux points \boldsymbol{x^+} et \boldsymbol{x^-},  separés arbitrairement d’une distance \boldsymbol{r}, on obtient après quelques manipulations:

(3)   \begin{equation*} \partial_t \langle (\delta \phi)^2 \rangle + \boldsymbol{\nabla_r} \cdot \boldsymbol{\Phi_r} + \boldsymbol{\nabla_X} \cdot \boldsymbol{\Phi_X} =0 \end{equation*}

In Eq. (3),

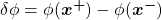  • \delta \phi =\phi (\boldsymbol{x^+}) - \phi (\boldsymbol{x^-})~~~~ est l’incrément (la différence) de 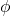\phi entre les deux points,
  • \langle (\delta \phi)^2 \rangle est appelée fonction de structure du second ordre de 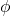\phi,
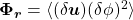  • \boldsymbol{\Phi_r} = \langle (\delta \boldsymbol{u})(\delta \phi)^2 \rangle est le flux of 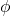\phi dans l’espace des échelles \boldsymbol{r}. Il traduit le processus de cascade d’une échelle à une autre.
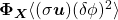  • \boldsymbol{\Phi_X}\langle (\sigma \boldsymbol{u})(\delta \phi)^2 \rangle est le flux de 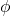\phi dans l’espace géométrique 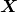\boldsymbol{X}, c’est à dire d’une position à une autre dans l’écoulement.
  • Les crochets désignent l’opérateur moyenne (qui peut dépendre de la situation)

Mesures géométriques intégrales

La littérature scientifiques des milieux poreux fait un usage extensif des statistiques en deux points de l’indicateur de phase. Un certain nombre de résultats analytiques permettent de relier \langle (\delta \phi)^2 \rangle aux propriétés géométriques de l’interface séparant le liquide du gaz. En particulier, aux petites échelles, le développement limité au troisième ordre s’écrit :

(4)   \begin{equation*} \langle (\delta \phi)^2\rangle_{\Omega} = \frac{\Sigma r}{2} \left[1 - \frac{r^2}{8} \left( \langle H^2\rangle_S - \frac{\langle G\rangle_S}{3} \right) \right] \end{equation*}

Dans l’Eq. (4)

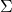  • \Sigma est la densité de surface de l’interface liquide-gaz.
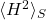  • \langle H^2\rangle_S est la moyenne pondérée par la surface de la courbure moyenne (au carré)
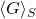  • \langle G\rangle_S est la moyenne pondérée par la surface de la courbure de Gauss
  • \langle \bullet \rangle_\Omega désigne la moyenne angulaire (selon toutes les directions du vecteur \boldsymbol{r})

Par conséquent, la limite aux petites échelles de l’Eq. (3) tend vers l’équation de transport de la densité de surface :

(5)   \begin{equation*} \partial_t \Sigma + \boldsymbol{u} \cdot \boldsymbol{\nabla_x} \Sigma = \mathbb{K} \Sigma \end{equation*}

où \mathbb{K} est le taux d’étirement. À plus grandes échelles, \langle (\delta \phi)^2\rangle est supposée rendre compte de la tortuosité de l’interface.

Simulation de l’instabilité de Plateau-Rayleigh par le code ARCHER. La surface est colorée par la courbure moyenne H.

(top) Simulation of homogeneous decaying liquid-gaz turbulence. (bottom) Simulation of liquid-gas shear flow. Both were carried out using the ARCHER code

Écoulements explorés

Turbulence diphasique homogène décroissante

Ce cadre analytique a tout d’abord été testé pour une turbulence homogène diphasique en décroissance. L’homogénéité statistique implique que les gradients selon \boldsymbol{X} sont nuls, reduisant ainsi le problème à une analyse temps/échelle de l’évolution du système (un problème 4D qui dépend de \boldsymbol{r} and t).

Résultats:

– Mise en évidence d’une échelle caractéristique basée sur la densité de surface et le volume de liquid qui traduit l’évolution en échelle de \langle (\delta \phi)^2\rangle
– Preuve que le taux d’étirement \mathbb{K} pilote le taux de transfert dans la cascade de \phi en parfaite analogie avec le taux de dissipation scalaire pour la cascade d’un traceur passif diffusif.

Ces résultats sont publiés dans Journal of Fluid Mechanics:

F. Thiesset, B. Duret, T. Ménard, C. Dumouchel, J. Reveillon, F.-X. Demoulin. 2020. Liquid transport in scale space. J. Fluid Mech. 886, A4.
Turbulence cisaillée liquide-gaz

Ce cadre théorique a ensuite permis d’explorer l’évolution temporelle d’une couche cisaillée liquide-gaz. Dans cette situation, l’homogénéité s’applique seulement selon deux directions et on doit alors recourir à la version 5D du budget espace/temps/échelle (3 dimensions pour \boldsymbol{r}, 1 direction d’inhomogénéité, 1 dimension de temps).

Résultats:

– La complexité du transport de liquide dans un espace combiné échelles/positions est mise en évidence.
– Mise en évidence d’une cohabitation entre un mécanisme de cascade directe (des grandes vers les petites échelles) ou d’une cascade inverse selon la gamme d’échelle et la position dans l’écoulement.

Les résultats ont été présenté à la conférence ILASS:

F. Thiesset, C. Dumouchel. T. Ménard, 2021. Space-scale-time dynamics of liquid–gas shear flow. J. Fluid Mech 912, A39
F. Thiesset, T. Ménard, C. Dumouchel. 2019. A New Theoretical Framework for Characterizing the Transport of Liquid in Turbulent Two-Phase Flows. ILASS-Europe, Paris, France.