Interaction de la lumière avec un objet de forme quelconque de surface lisse et ses applications à la métrologie optique.
Context :
La diffusion de la lumière par des particules ou objets de taille importante et de forme irrégulière est à la fois un défi théorique et un verrou pour beaucoup d’applications, comme la métrologie optique des sprays et des jets liquides. La communauté scientifique ne connait aucun moyen pour prédire avec précision leurs grandeurs physiques de façon générale. En effet, il existe bien des méthodes numériques, mais elles sont limitées à des objets de petite taille (quelques dizaines de longueurs d’onde). Des théories analytiques existent également (solution des équations de Maxwell), mais elles ne s’appliquent qu’à des objets de forme simple (sphère, ellipsoïde, etc.). Et, même dans ce cas, la taille calculable n’est pas non plus très grande si l’objet n’est pas sphérique. On peut également utiliser l’optique géométrique classique, qui est souple et peut être appliquée à des objets de grande taille, mais sa précision n’est pas suffisante pour beaucoup d’applications.
Toutes ces contraintes sont très limitatives : les particules/objets rencontrés dans les processus réels sont bien souvent de forme complexe et de taille importante.
Partant de ce constat et motivé par l’enjeu scientifique et l’intérêt pratique, nous développons au sein du laboratoire depuis presque deux décennies un nouveau modèle d’optique géométrique, basé sur la propagation de rayons. Aujourd’hui, les fondamentaux du modèle sont établis et des applications sont en développement.
Développement du modèle :
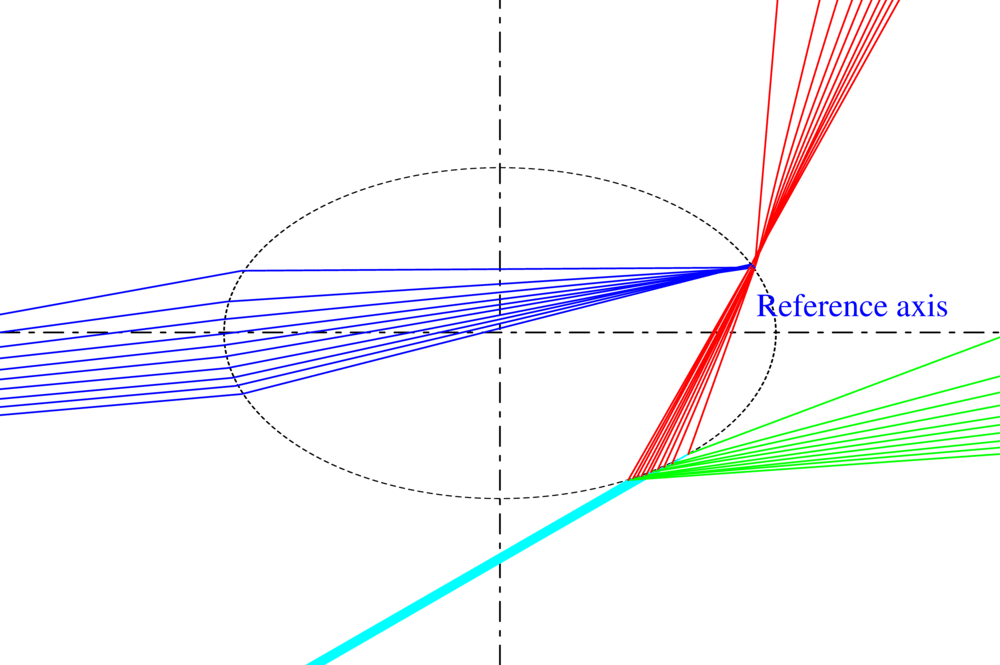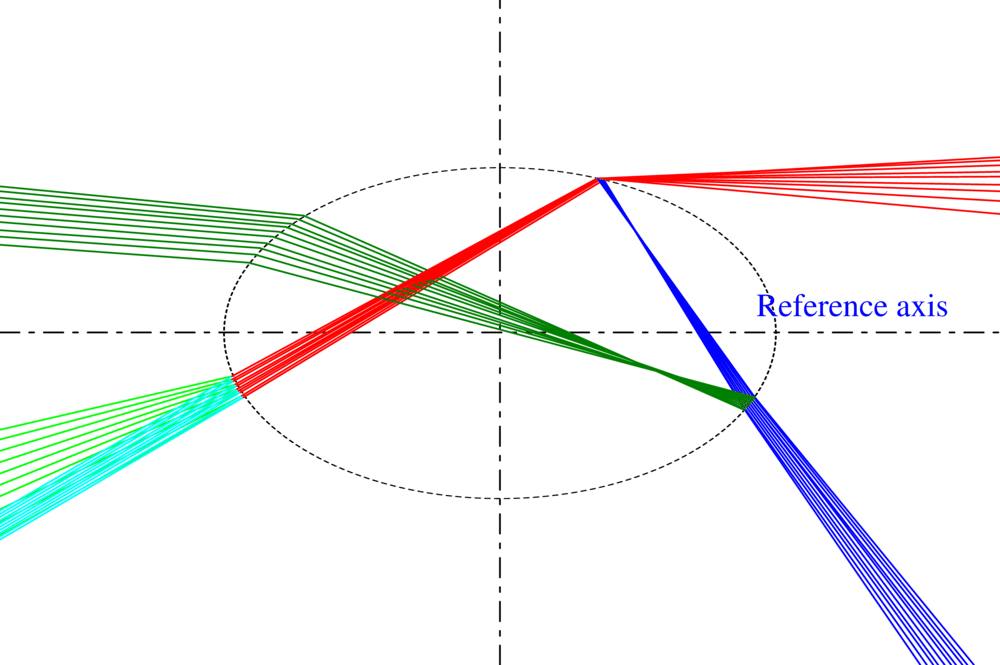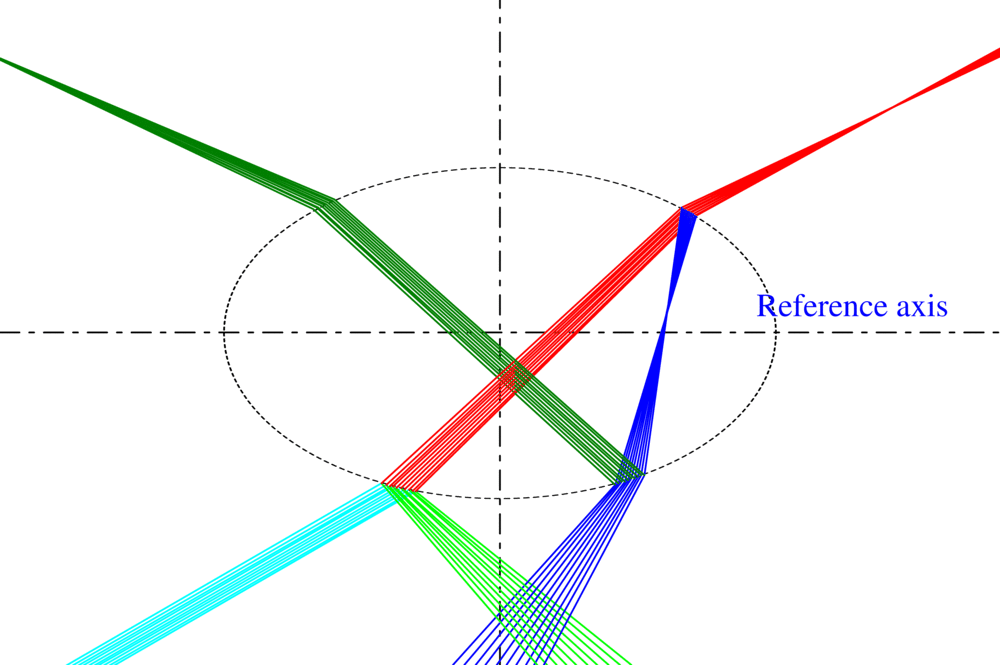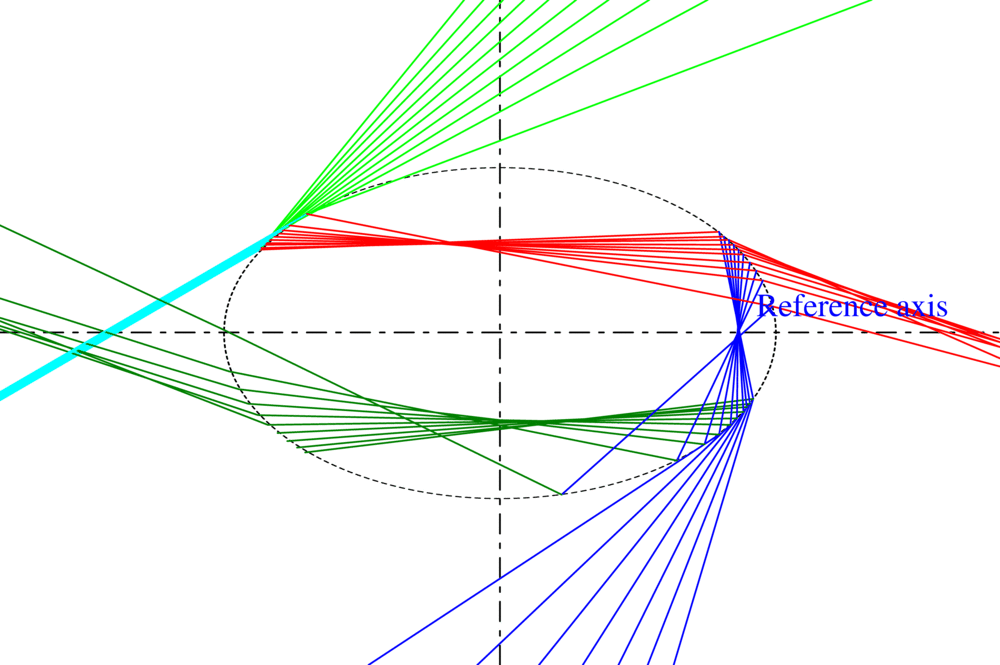
La notion de rayon lumineux dans l’optique géométrique traditionnel ne permet pas de décrire la divergence ou convergence de l’onde qu’il représente. Pour remédier à ce défaut, nous avons introduit la courbure du front d’onde comme une propriété intrinsèque du rayon lumineux. On aboutit à un modèle original, appelé VCRM (Vectorial Complex Ray Model en anglais) qui permet de prédire facilement la divergence ou la convergence de l’onde lorsqu’elle interagit avec une surface courbée (réfléchie ou réfractée), ainsi que la phase due aux lignes focales. De plus, en exprimant la direction des rayons et les formules de Fresnel par les vecteurs d’onde et ses composantes, le VCRM facilite considérablement le calcul. De nombreuses validations ont été faites :
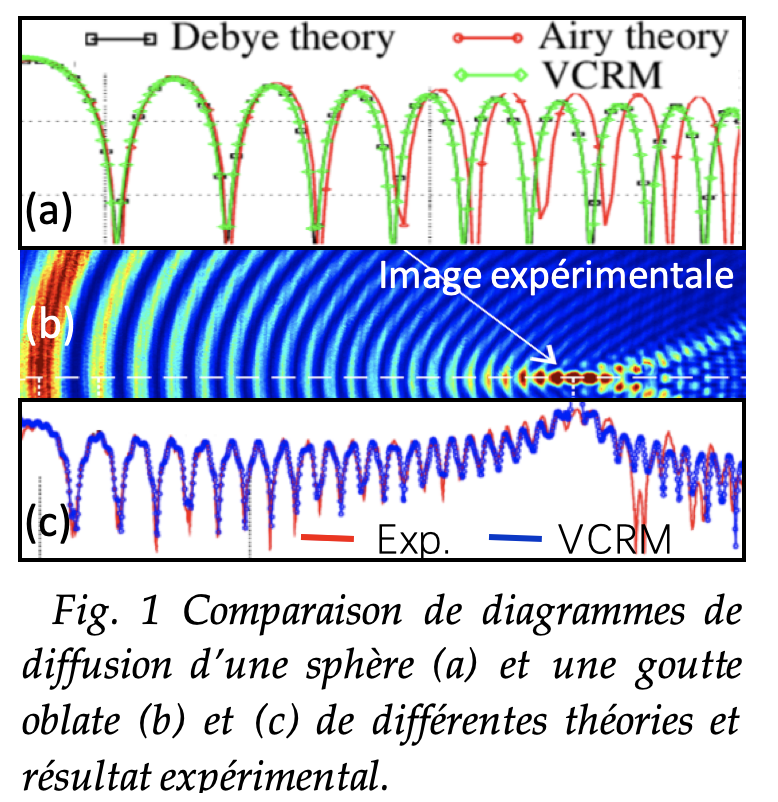
- Pour une sphère, en comparant avec la méthode rigoureuse de Debye, VCRM prévoit mieux la structure d’Airy que la théorie d’Airy (Fig. 1 (a)).
- Pour un sphéroïde, la simulation de VCRM est en bon accord avec les résultats expérimentaux (Fig. 1 (b) and (c)).
- Les résultats de VCRM ont été aussi validés par comparaison avec la méthode numérique MLFMA.
Applications à la métrologie optique :
Le VCRM pouvant prédire le diagramme de diffusion d’un grand objet de surface lisse de forme quelconque comme les gouttes, les filaments et les nappes de liquide, nous pouvons l’utiliser pour déduire les propriétés (forme, taille, température, …) de ces objets. Voici trois exemples d’applications à la métrologie optique :
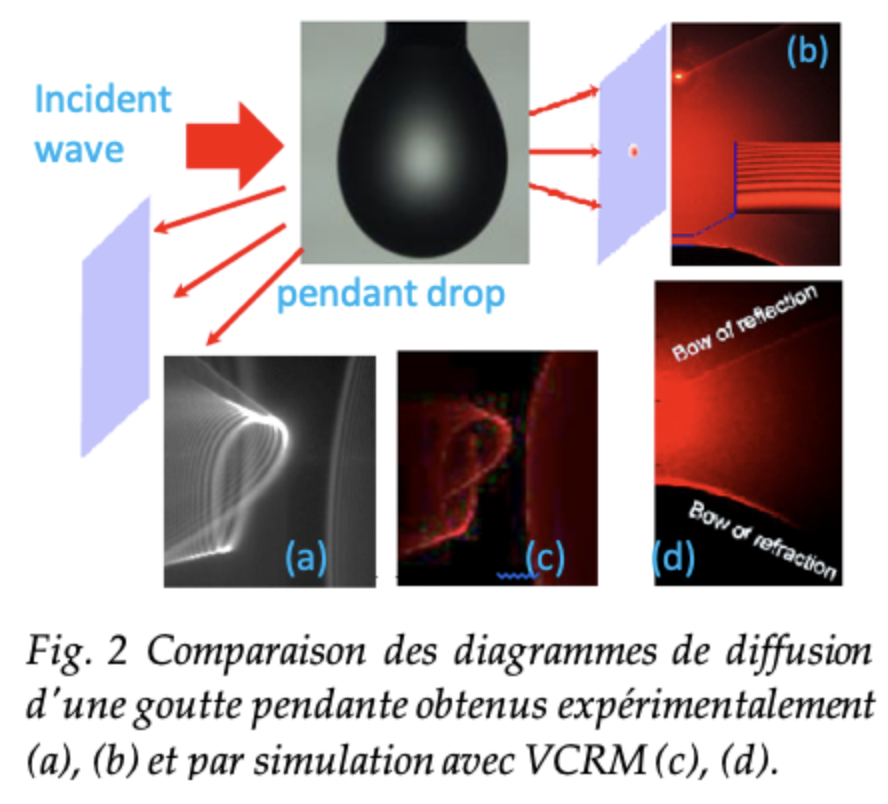
- Comparaison numérique-expérimentale de diagrammes de diffusion en 3D d’une goutte pendante (Fig. 2).
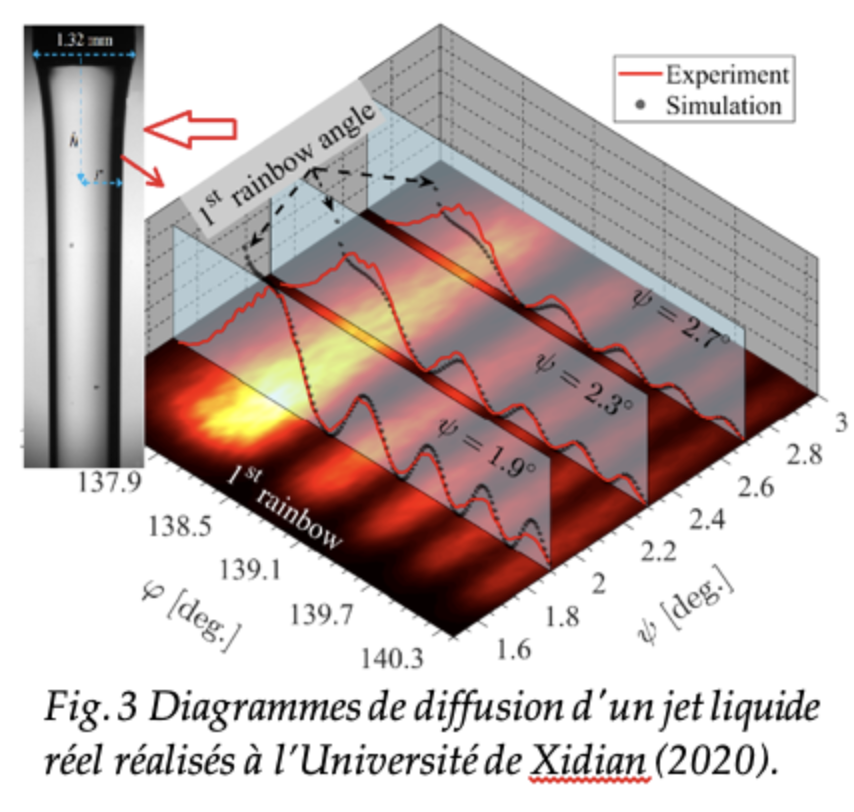
- Caractérisation d’un jet liquide réel par ses diagrammes de diffusion (Fig. 3).
- Imagerie d’un objet : le VCRM permet aussi de prédire l’image d’un objet de forme quelconque (jet de liquide, ligament, nappe liquide …).
Logiciels à télécharger :
ABsphere : http://amocops.univ-rouen.fr/en/content/download
VCRMEll2D: http://amocops.univ-rouen.fr/en/content/download
Références :
- K. F. Ren, F. Onofri, C. Rozé and T. Girasole, « Vectorial complex ray model and application to two-dimensional scattering of plane wave by a spheroidal particle », Opt. Lett. 36(3): 370-372, 2011 lien
- F. Onofri, K. F. Ren, M. Sentis, Q. Gaubert, and C. Pelcé, « Experimental validation of the vectorial complex ray model on the inter-caustics scattering of oblate droplets », Opt. Express 23(12), 15768-15773, 2015 lien
- M. Yang, Y. Wu, X. Sheng and K. F. Ren, « Comparison of scattering diagrams of large non-spherical particles calculated by VCRM and MLFMA », J. Quant. Spectrosc. Radiat. Transfer 162:143-153, 2015 lien
- Q. Duan, X. Han, S. Idlahcen, K. F Ren, “Three-dimensional light scattering by a real liquid jet: VCRM simulation and experimental validation”, JQRST 239 (2019) 106677 lien





