Interaction of light with an object of any shape of smooth surface and its applications to optical metrology.
Context
The scattering of light by large and irregularly shaped particles or objects is both a theoretical challenge and a barrier for many applications, such as optical metrology of sprays and liquid jets. The scientific community does not have any means to accurately predict the physical quantities of scattering in general. Indeed, there are many numerical methods, but they are limited to small objects (size of few tens of wavelengths). Analytical theories also exist (solution of Maxwell’s equations), but they only apply to objects of simple shape (sphere, ellipsoid, etc.). And, even in this case, the calculable size is also not very large if the object is not spherical. Classical geometric optics may be used, which is flexible and can be applied to large objects, but its accuracy is not sufficient for many applications.
All these constraints are very limiting: the particles / objects encountered in real processes are very often of complex shape and large size.
Based on this observation and motivated by the scientific challenge and practical interest, we have been developing in the laboratory since almost two decades a new geometric optical model, based on the propagation of rays. Today the fundamentals of the model are established and applications are under development.
Model developpment :
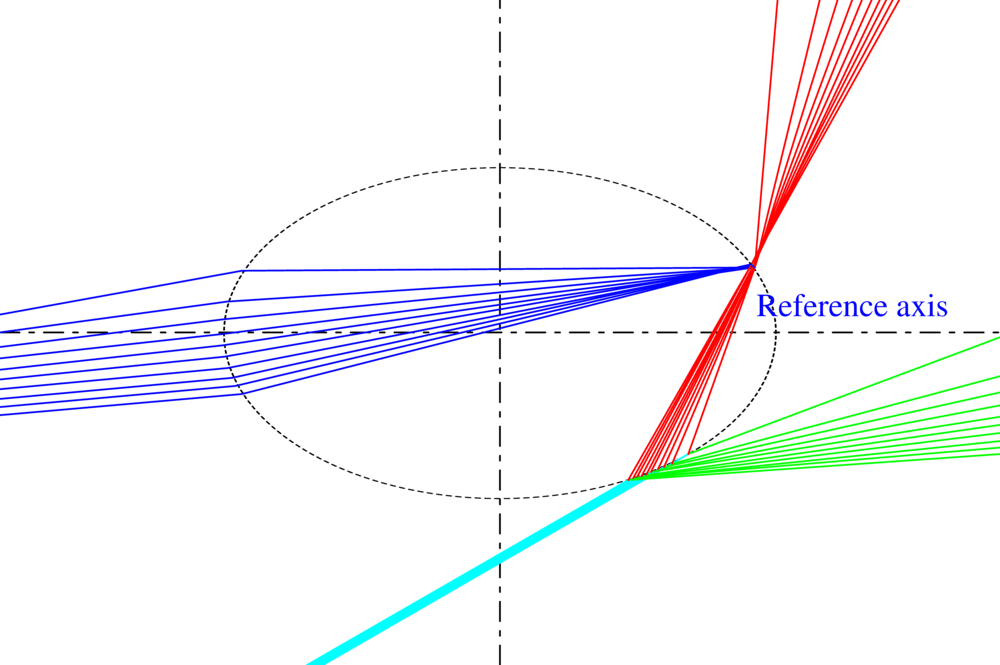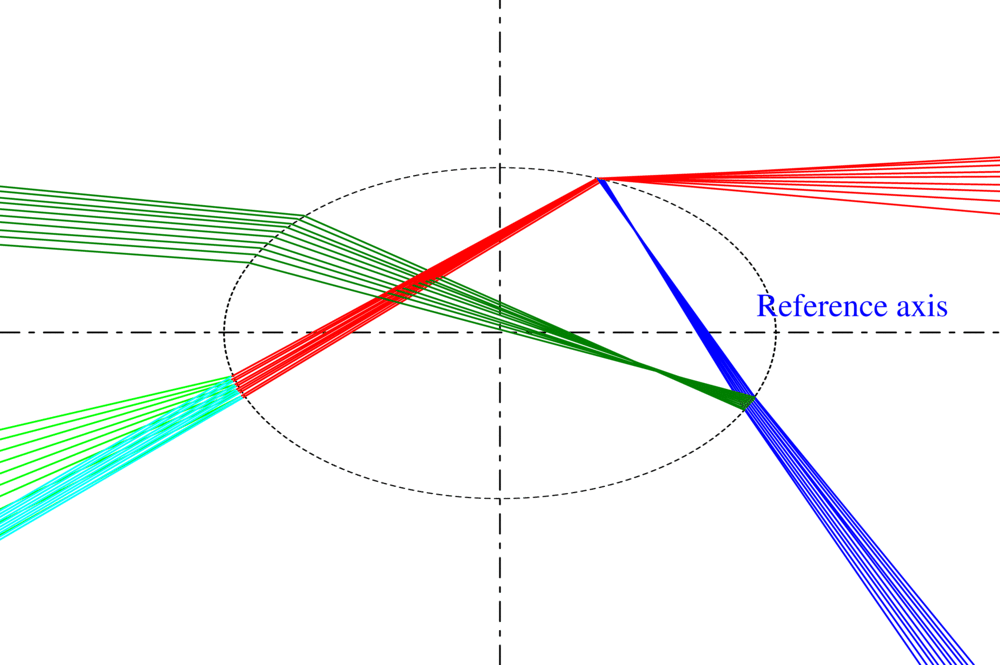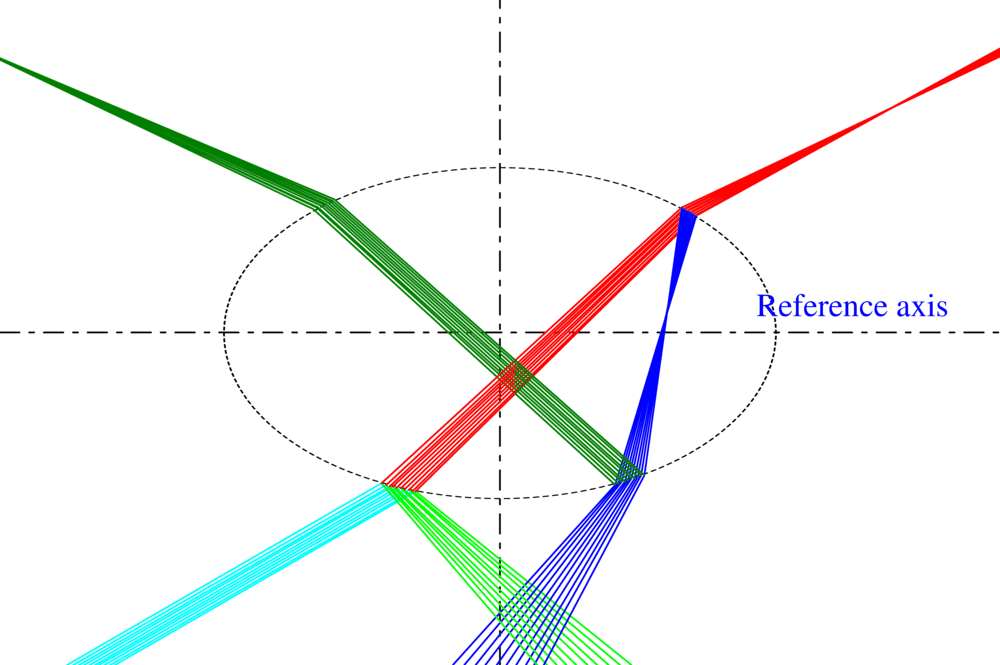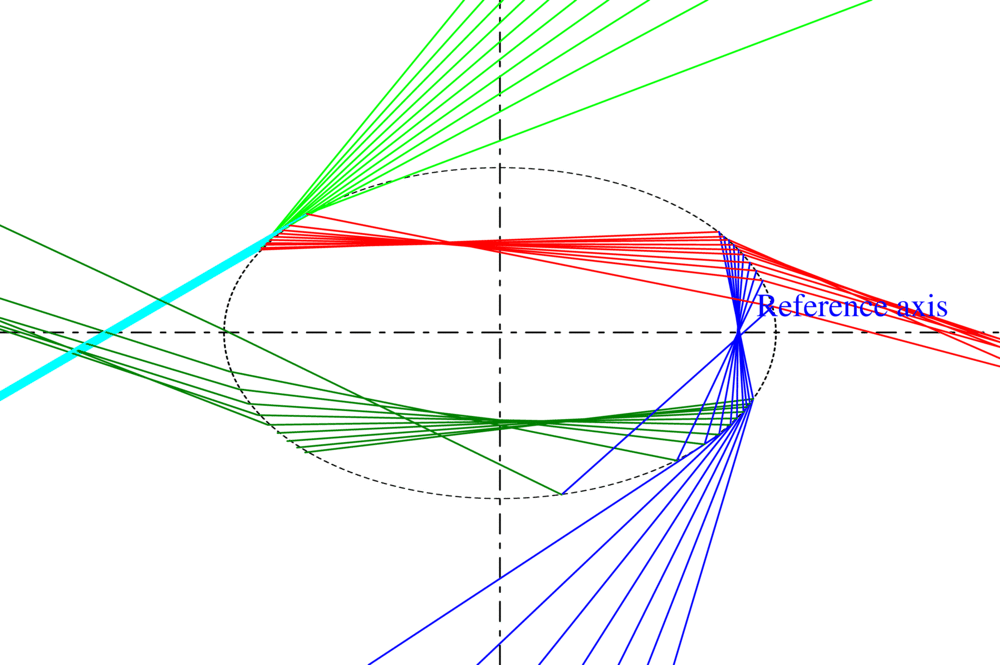
The notion of ray in traditional geometric optics does not allow to describe the divergence or convergence of the wave it represents. To remedy this flaw, we have introduced the curvature of the wavefront as an intrinsic property of the ray and developed an original model, called VCRM (Vectorial Complex Ray Model). VCRM makes it possible to easily predict the divergence or convergence of the wave when it interacts with a curved surface (reflected or refracted), as well as the phase due to focal lines. In addition, by expressing ray direction and Fresnel formulas by wave vectors and its components, VCRM simplifies considerably the calculation. Many validations have been carried out:
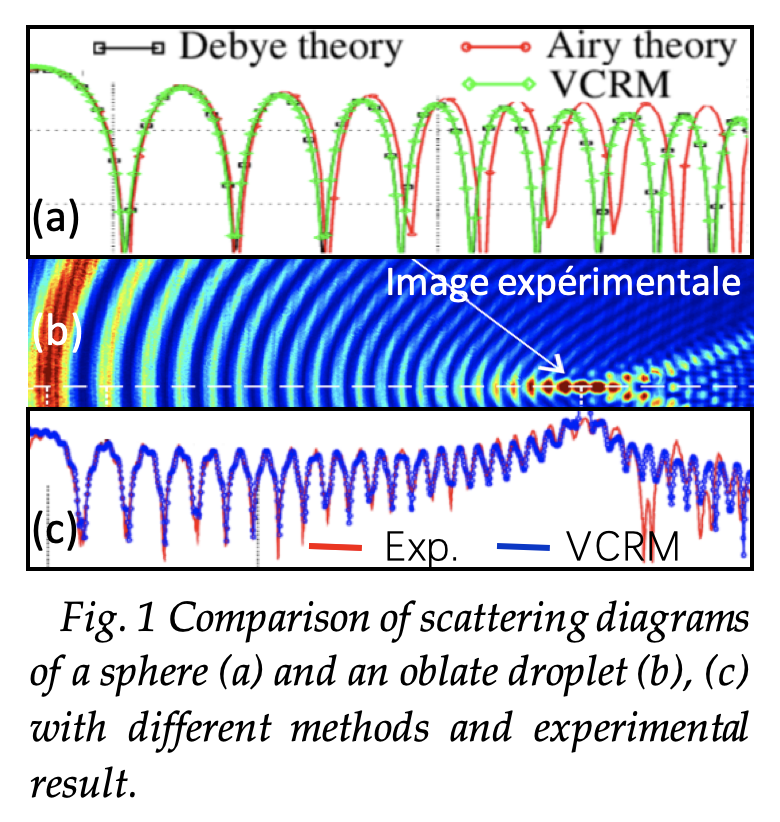
- For a sphere, in comparison with the rigorous method of Debye, VCRM predicts the structure of Airy better than the theory of Airy (Fig. 1 (a)).
- For a spheroid, the VCRM simulation is in good agreement with the experimental results (Fig. 1 (b) and (c)).
- The results of VCRM were also validated by comparison with the numerical method MLFMA (multilevel fast multipole algorithm).
Application to the optical metrology:
Since VCRM can predict the scattering diagram of a large object with a smooth surface of any shape such as drops, filaments and liquid films, we can use it to deduce properties (shape, size, temperature, etc.) of this kind of objects. We cite here three examples of applications in optical metrology:
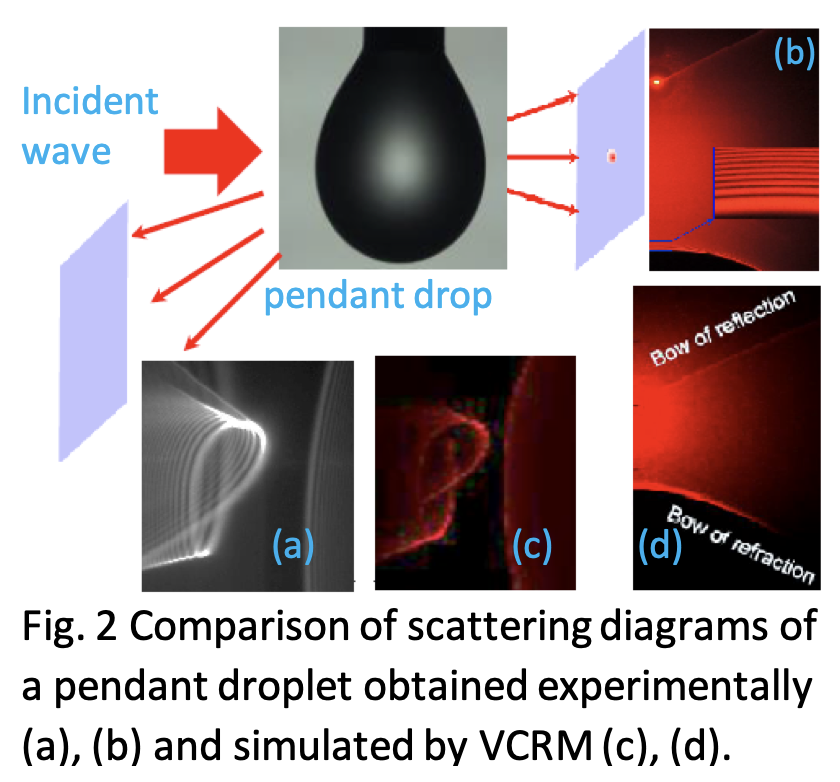
- Numerical-experimental comparison of 3D scattering diagrams of a pendant drop (Fig. 2).
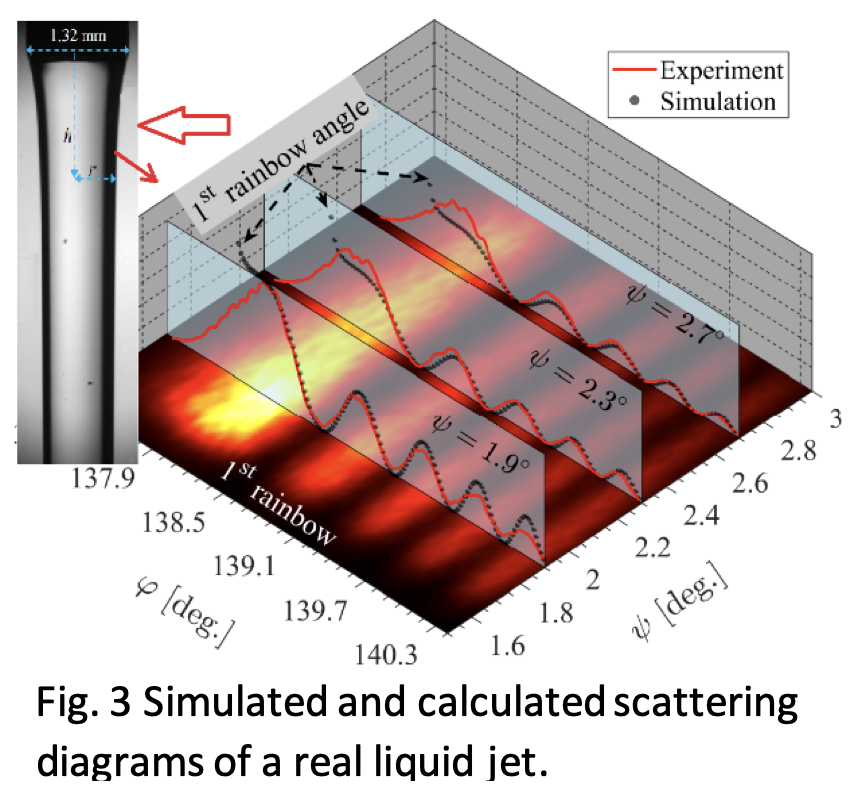
- Characterization of a real liquid jet by its scattering diagrams (Fig. 3).
- Imaging of an object: VCRM can also predict the image of an object of any shape (jet of liquid, ligament, liquid film, etc.).
Software to be download
ABsphere : http://amocops.univ-rouen.fr/en/content/download
VCRMEll2D: http://amocops.univ-rouen.fr/en/content/download
References :
- K. F. Ren, F. Onofri, C. Rozé and T. Girasole, “Vectorial complex ray model and application to two-dimensional scattering of plane wave by a spheroidal particle", Opt. Lett. 36(3): 370-372, 2011 lien
- F. Onofri, K. F. Ren, M. Sentis, Q. Gaubert, and C. Pelcé, “Experimental validation of the vectorial complex ray model on the inter-caustics scattering of oblate droplets", Opt. Express 23(12), 15768-15773, 2015 lien
- M. Yang, Y. Wu, X. Sheng and K. F. Ren, “Comparison of scattering diagrams of large non-spherical particles calculated by VCRM and MLFMA", J. Quant. Spectrosc. Radiat. Transfer 162:143-153, 2015 lien
- Q. Duan, X. Han, S. Idlahcen, K. F Ren, “Three-dimensional light scattering by a real liquid jet: VCRM simulation and experimental validation”, JQRST 239 (2019) 106677 lien





