The CORIA lab shared ressources are:
- RENADIAG, for metrological ressources.
- its numerical department and their softwares and libraries for HPC.
Metrological ressources from RENADIAG

RENADIAG TOFU
RENADIAG TOFU (tracking of ultrafast phenomena) is an innovative experimental platform dedicated to the use of ultrafast laser sources for the detection and tracking of ultrafast or rare events. This optical metrology platform, funded by the Normandy region and the European Union, relies on CORIA’s know-how in the design and use of laser sources, notably based on optical fibres, at different wavelengths in the near (NIR) and medium infrared (MIR). Through this platform, the laboratory has unique means for the preparation of specialty optical fibres and for the realisation of original ultrafast imaging techniques based on these fibres as well as for their characterisation.


RENADIAG MDA (Aerosol Metrology)
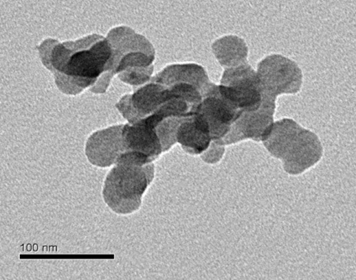
The laboratory has, in the optics and lasers department, an advanced experimental platform for the generation and characterization of soot and other aerosols The size distribution of nanoscale aerosols can be accessed by ex-situ (SMPS) or in-situ (angular scattering) measurements. Mass or volume concentrations are also accessible after sampling (PPS Pegasor) or in-situ (Laser Induced Incandescence). It is also possible to take samples of particles by controlling the dilution and perform morphological analyses of them on the basis of electron microscopy (TEM) images. Classification devices by mass (CPMA), mobility diameter (DMA), aerodynamic diameter (AAC) are also available.
| Responsable: | Jérôme Yon |
| Scientific project: | Experimental characterization of soot particles |
| Founding: | platform supported by the Normandie region |
Numerical facilities
| Responsable: | Ghislain Lartigue |
| Scientific project: | Vincent Moureau: |
| Modélisation de la combustion turbulente prémélangée |
ARCHER
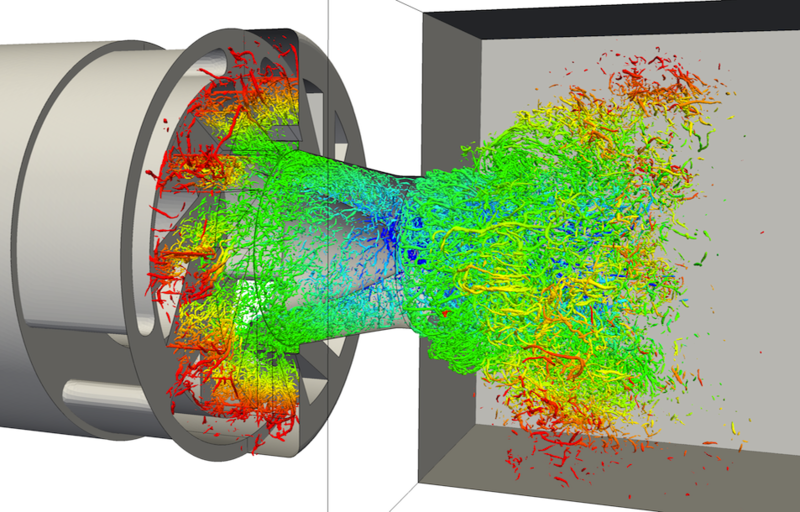
ARCHER is a High-Performance-Computing code developed at the CORIA laboratory. It stands for Academic Research Code for Hydrodynamic Equations Resolution. It also takes its name from the fish, the archerfish (Toxotidae), known for preying insects by spitting a jet of water.
ARCHER is aimed at carrying Direct Numerical Simulations of two-phase flows may they be turbulent, incompressible or compressible, with phase change or in presence of solid boundaries. Data from Archer are used for probing the physical properties (either geometrical, morphological, topological, or dynamical) of different phenomena such as atomization, spray formation, dispersion, evaporation, phase separation, capture of solid aerosols. The close connection of the Archer developers with experimentalist is further noticeable. This wide knowledge serves for building or reinforcing physics-informed models, notably the Eulerian Lagragian Spray Atomization model (ELSA).
It was one of the first code worldwide, undertaking the simulation of liquid-jet atomization under a realistic injection configuration.
| Responsable: | Alexandre Poux |
| Scientific project: | Thibaut Ménard: |
| The ARCHER code |
MCAC
| Responsable: | Alexandre Poux |
| Scientific project: | Jérôme Yon: |
| Formation and morphological caracterization of aggregates of nanoparticles |





