Contact :
Marie Charlotte Renoult, associate professor
Context
Ferrofluids are liquids exhibiting strong magnetic properties. Because ferromagnetic materials lose their magnetic properties at liquid state, ferrofluids need to be synthesized. They are obtained by dispersing nanoparticles of magnetite into a liquid phase and by incorporating a surfactant to prevent the agglomeration of the particles. Ferrofluids are used in many fields, frequently under the form of jets and drops. These jets and these drops are controlled with the help of a magnetic field. This is the case, for example, in the printing field where the magnetic ink is shifted towards a surface, and in medicine where the drug carried by the ferrofluid is directed towards the place to cure, thanks to a magnetic field. In order to predict the behaviours of ferrofluid jets, especially the breakup into drops, a stability analysis can be realised. Because the instability is developing along the axis of the jet, a spatial stability analysis is required. Nevertheless, for sufficiently high jet velocities, the temporal stability analysis of an infinite length cylinder allows to retrieve the main characteristics of the jet instability. In the literature, many temporal stability analysis of ferrofluid cylinders under a magnetic field are identified. These ones are focused on particular magnetic field shapes with inviscid ferrofluids. However, ferrofluids can have a viscosity one order of magnitude higher than the one of water and it must be taken into account.
This theoretical study on ferrofluid jets is supported by LabEx through the INFEMA (INstabilities of FErrofluid flows in MAgnetic fields) project common between the two Norman laboratories CORIA (UMR 6614) and LOMC (UMR 6294 – Le Havre).

Ferrofluid synthesized at the laboratory, near a magnet.

Ferrofluid cylinder under a magnetic field ![]() .
.
Viscous theory
An incompressible Newtonian ferrofluid cylinder under a steady axisymmetric magnetic field is considered. The ferrofluid is placed under isothermal conditions with no gravity. A linear stability analysis of this system is realised by imposing a small amplitude axisymmetric disturbance. The magnetic fields admitted by these assumptions can be divided into two groups: axial and non-axial magnetic fields. For this last case, a cylindrical structure, which can be a wire, is necessary at the ferrofluid cylinder center to overcome a singularity. A dispersion relation valid for all the admissible magnetic fields is obtained for the two cases by considering, as a first step, negligeable viscosity and density for the surrounding fluid. Two magnetic field shapes are mainly studied in the literature : the axial and azimuthal ones. The stabilizing effects of the magnetic field for these two cases are retrieved with a total stability above a critical value of the magnetic field intensity for the azimuthal shape. A third case destabilizing the ferrofluid cylinder and allowing a control on the dispersion relation is found. The imposed magnetic field must have, in this case, a radial component. Finally, a dispersion relation which takes into account the density and the viscosity of the surrounding fluid is also obtained for the azimuthal magnetic field case.
Azimuthal case
An azimuthal magnetic field is under the form ![]() where
where ![]() is a constant. It can be created with an electric current passing through a wire at the center of the ferrofluid cylinder. This wire is also used to overcome the singularity at
is a constant. It can be created with an electric current passing through a wire at the center of the ferrofluid cylinder. This wire is also used to overcome the singularity at ![]() . The azimuthal magnetic field has a stabilizing effect on the ferrofluid cylinder with a decrease of the growth rate of the most unstable mode as the magnetic field intensity increases. The cylinder becomes stable for all wavenumbers above a critical value of the magnetic field. Taking into account the ferrofluid viscosity allows to be closer to the experimental data than with the inviscid theory. However, the difference with the experimental data is still high and a correct prediction of these data can only be obtained by considering the surrounding fluid viscosity.
. The azimuthal magnetic field has a stabilizing effect on the ferrofluid cylinder with a decrease of the growth rate of the most unstable mode as the magnetic field intensity increases. The cylinder becomes stable for all wavenumbers above a critical value of the magnetic field. Taking into account the ferrofluid viscosity allows to be closer to the experimental data than with the inviscid theory. However, the difference with the experimental data is still high and a correct prediction of these data can only be obtained by considering the surrounding fluid viscosity.
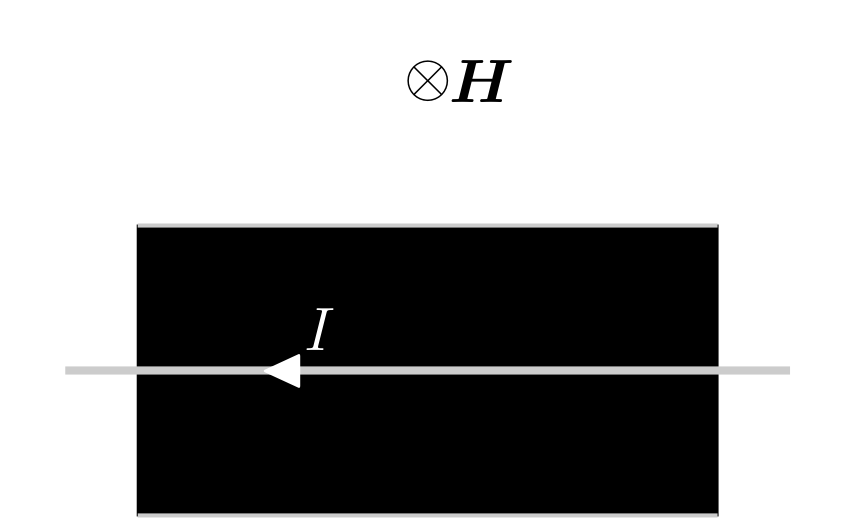
Representation of the configuration with an azimuthal magnetic field.
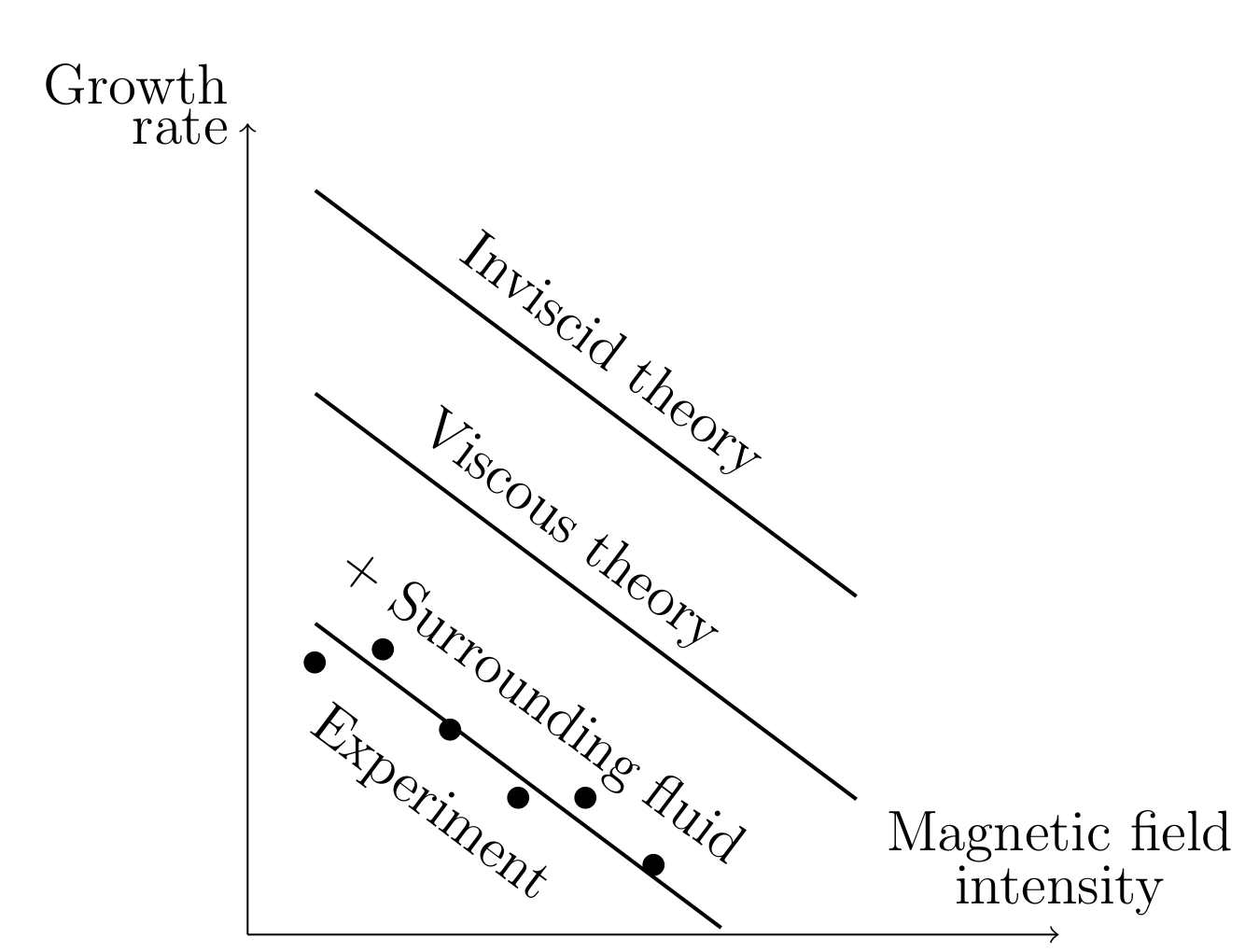
Growth rate of the most unstable mode as a function of magnetic field intensity.
New experiments and new theory
In order to remove uncertainties regarding the experimental data of the literature and to obtain new data to compare with the theoretical stability analysis, new experiments were performed at the laboratory. The ferrofluid column is maintained around a hollow copper wire with a high azimuthal magnetic field created by an electric current passing through this wire. Water flows inside the wire in order to dissipate the heat produced by Joule effect. The whole is immersed inside a cuvette full of glycerol with the same density as the one of ferrofluid in order to neglect the gravity effect. Then, the magnetic field intensity is decreased to destabilize the ferrofluid column.
These experiments were realized for different magnetic field intensities and different ratio between the radius of the wire and the radius of the ferrofluid column. A discrepancy was observed between the experimental data and the theory et we noticed that temperature regulation with the water cooling of the wire was not optimal.
Thus, a new theoretical stability analysis was developed by taking into account thermocapillary effects. This theory shows that the discrepancy with the experimental data can be explained with the thermocapillary effects and that these ones have a great impact on the stability when a temperature gradient is present.


Deformation of a ferrofluid column around a copper wire without magnetic field (top) and with magnetic field (bottom) for different ratio between the radius of the wire and the radius of the ferrofluid column (low ratio on the left and high ratio on the right).


People
- Marie-Charlotte Renoult (associate professor)
- Romain Canu (post-doc and then researcher)
- Antoine Andrieu (undergraduate student)
- Antoine Bouchet (undergraduate student)
Scientific production
- 1 poster for the Rencontre du Non Linéaire 2020
R. Canu, M.-C. Renoult. Analyse linéaire de stabilité d’un jet de ferrofluide.
- 1 presentation for the APS-DFD 2020
R. Canu, M.-C. Renoult. Control of ferrofluid jets with magnetic fields.
- 1 poster for the Rencontre du Non Linéaire 2021
R. Canu, M.-C. Renoult. Analyse faiblement non-linéaire de stabilité d’un cylindre de ferrofluide.
- 1 presentation for the EFMC 2022
- 2 papers published to Journal of Fluid Mechanics and 1 paper published to Physics Of Fluids





